Já precisou saber o número de combinações para um determinado grupo de valores?
Este tipo de conta é fácil de fazer no papel ou até mesmo de cabeça quando, por exemplo, o grupo de elementos é reduzido. Por exemplo: Quantos pares diferentes e não repetidos é possível formar em um grupo de 3 elementos? Imagine que estes elementos sejam as primeiras 3 letras do alfabeto. Assim podemos fazer AB, AC e BC.
Pronto, nossa resposta é 3 pares únicos. Agora, se quisermos permitir a repetição e valores, a resposta é 6: AB, AC, BC, BA, CA e CB.
Complicou um pouquinho? Então imagine você ter de calcular o número de possibilidades que um volante da Mega-Sena, que possui 60 números, oferece. A não ser que você seja bom com números essa vai ser uma tarefa complicada, certo? Mas, com nosso querido Excel vamos resolver isso em questão de segundos.
A fórmula que vamos utilizar é a =Combin(número total de elementos; número de elementos por grupo) para combinações que NÃO repetem elementos, ou então =Combina(número total de elementos; número de elementos por grupo) para quando você QUER REPETIR elementos no grupo.
Ficou complicado, então vamos a alguns exemplos.
No exemplo abaixo vou pedir para o Excel me retornar o número de combinações em duplas não repetidas que podemos formar em um grupo total de 10 elementos. Para visualizar o exemplo imagine com letras novamente. Temos A, B C, D, E, F, G, H, I, J como grupo de elementos e como desejamos duplas não repetidas vamos ter AB, AC, AD.... IJ.
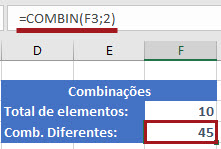
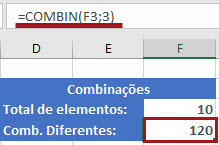
Reparou na fórmula? Vejaque no campo "número total de elementos" eu fiz referência à célula que continha esse dado e depois inseri o valor "2" no campo "número de elementos por grupo". Ou seja, com esse "2" eu informei ao Excel que desejo calcular duplas. Se eu quisesse trios, por exemplo, ABC, DEF, GHI... eu colocaria o "3".
Veja o resultado:
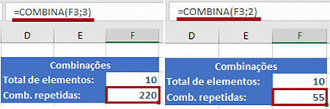
Até aqui vimos as combinações que não se repetem, mas se quisermos saber as combinações permitindo os repetecos, é só a função =Combin em =Combina. Veja:
Agora que já sabemos como usar as funções estamos prontos para calcular as combinações de um volante da Mega-Sena que deixamos em aberto desde o início do texto. Vamos usar a =Combin(), pois, como sabemos, na Mega os números não podem repetir. Já no campo de "número de elementos" vamos inserir o 6, pois este é a quantidade de números sorteados por vez, ou seja, as combinações devem ser de 6 em 6 números.
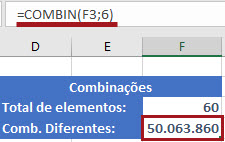
Sim amigos, são mais de 50 milhões de combinações, ou seja, se você fizer apenas 1 jogo de 6 dezenas você tem 1 chance em mais de 50 milhões de ganhar. Desculpa pelo balde de água fria, mas vai ser difícil ficar rico na loteria, melhor chegar lá atrás de estudo e trabalho duro. E para encurtar esse caminho é só clicar na imagem aqui embaixo e conhecer nossa plataforma de estudos online.


